Varianza: Qué es y cómo se calcula

Descubre las claves de la varianza: qué es, cómo se calcula y de qué forma puede ayudarte a entender mejor los datos de tu negocio. Un concepto con múltiples aplicaciones en el mundo de la estadística.

• La varianza es una medida de dispersión.
• En el ámbito financiero, traslada la idea del riesgo.

La varianza es un concepto estadístico que nos permite entender mejor los datos. Además, nos ofrece múltiples capas a las que podemos aproximarnos. Desde un punto de vista intuitivo, ayuda a comprender la noción de dispersión. Desde uno más formal, permite múltiples aplicaciones en el ámbito de la estadística.

De cualquier forma, en un mundo gobernado por los datos, es una de las primeras nociones estadísticas que nadie debe obviar. En el ámbito empresarial, contribuye a expresarnos mejor y extraer con más facilidad conclusiones útiles de diferentes clases de informes. No tener unos conocimientos mínimos constituye una suerte de analfabetismo estadístico.

Qué es la varianza

En términos de estadística descriptiva, la varianza puede ser definida como la media de los cuadrados de las desviaciones sobre la media. A partir de esta definición, nos puede surgir la duda de por qué calculamos una media de cuadrados de las desviaciones y no de las desviaciones en sí.

La respuesta es sencilla. Una de las propiedades de la media, de cualquier media, es que la media de las desviaciones sobre la media es siempre cero. Por eso, recurrimos a la varianza, a veces también denominada momento de segundo orden centrado en la media.

La media de las desviaciones sobre la media siempre es cero.

Pongamos un ejemplo. Imaginemos que queremos calcular la media de 8, de 9 y de 10. Solo tendremos que efectuar la suma (que nos dará 27) y dividir entre 3. Vemos que la media es 9. Las desviaciones serán -1,0 y 1. La media de las desviaciones es 0. Tomemos los valores que tomemos, el resultado será siempre el mismo.

Elevar al cuadrado las desviaciones antes de tomar la media es, por tanto, un remedio para evitar que este cálculo sea siempre cero. Recordemos que tanto si la desviación es positiva como si es negativa o cero, el cuadrado nunca es negativo. La suma será mayor o igual que cero. Solo será cero cuando todos los valores sean iguales y, por lo tanto, no haya ninguna desviación de la media.

No obstante, al elevar al cuadro también elevamos al cuadrado las unidades en las que medimos la varianza. Por ejemplo, si la media es en metros, la varianza se medirá en metros cuadrados. Para evitar este problema, podemos extraer la raíz cuadrada de la varianza, denominada desviación típica, que se emplea en muchas situaciones.

La desviación típica es la raíz cuadrada de la varianza.

¡Comparte! La varianza es uno de los conceptos fundamentales de la estadística. Te enseñamos a comprenderlo.

Cómo calcularla

Si tenemos un conjunto de datos de la variable X, su varianza la podemos calcular como:

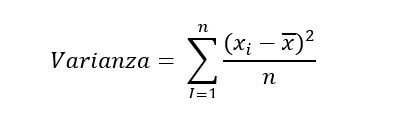
Donde:

Varianza de una variable aleatoria

En el cálculo de probabilidades, también nos puede interesar calcular la varianza de una variable aleatoria. Para ello, procederemos del siguiente modo:

Donde:

• Var(X) es la varianza de la variable aleatoria discreta X.
• E es la esperanza matemática.

Si lo que tenemos es una variable aleatoria discreta, esto se transforma en:

Donde:

En el caso de una variable aleatoria continua, tendremos:

Donde:

• E(X) es la esperanza matemática de la variable aleatoria X.
• f(x) es la función de densidad de probabilidad de la variable aleatoria X.

Qué mide la varianza

La varianza es una medida de dispersión. Eso significa que pretende capturar en qué medida los datos están en torno a la media. Si tenemos datos muy por encima y muy por debajo de la media, esta será menos representativa y lo veremos reflejado en una elevada varianza.

Imaginemos, por ejemplo, que queremos calcular el salario medio de dos empresas de solo dos trabajadores. En la empresa A, los salarios son de 24.500 y 23.500 euros. En la B, son de 16.000 y 32.000 euros. Vemos que, en ambos casos, la media es la misma: 24.000 euros. Sin embargo, esa media es más representativa en la empresa A, ya que los 2 valores se encuentran mucho más próximos a la media que en la empresa B.

En nuestro sencillo ejemplo, no nos ha hecho falta calcular la varianza para observar, de un vistazo, que la media es más representativa en la empresa A. No obstante, podríamos haber tenido cientos, miles, millones de datos… En ese caso, nos es útil tener una cifra que nos muestre la dispersión.

Sin embargo, la varianza, por sí sola, tampoco nos dice demasiado. En nuestro ejemplo, estamos comparando dos empresas con la misma media, pero necesitamos un valor que nos ponga más en contexto. Al fin y al cabo, con distintas medias, es lógico que las varianzas difieran. La solución pasa por el coeficiente de variación:

Donde:

Este coeficiente tiene la ventaja de que es un tanto por uno y, por tanto, es adimensional. Mide cuántas veces la desviación típica (raíz cuadrada de la varianza) está contenida en la media.

Algunas aplicaciones de la varianza

Las aplicaciones estadísticas del concepto de la varianza son incontables. Las siguientes son solo algunas de las principales:

• Los estimadores eficientes. Son aquellos cuya esperanza es el verdadero valor del parámetro y, además, tienen una mínima varianza. De este modo, hacemos lo más pequeño posible el riesgo de que lo que extraemos de una muestra se aparte demasiado del verdadero valor del parámetro.
• Los estimadores consistentes. Son aquellos que, a medida que crece el tamaño de la muestra, tienden a tener una varianza de cero. Por lo tanto, con muestras grandes, la estimación tiende a desviarse muy poco del verdadero valor.
• En la distribución normal, la varianza (su raíz cuadrada, la desviación típica) es uno de los parámetros. La campana de Gauss tiende a ser más alta y estrecha a medida que la varianza disminuye.
• En modelos de regresión, hablamos de homocedasticidad cuando la varianza del error es constante a lo largo de sus observaciones. Por ejemplo, en una regresión simple, vemos una nube de puntos en la que la dispersión de los puntos alrededor de la recta o curva estimada se mantiene constante.
• El análisis de la varianza (ANOVA) permite comparar diferentes grupos y ver los factores que influyen en ellos.
• La desigualdad de Chebyshev nos permite acotar en qué medida es probable que una variable aleatoria se separe de su esperanza matemática en proporción a su desviación típica (raíz cuadrada de la varianza).

La varianza en finanzas

En finanzas, es habitual relacionar la varianza con el riesgo. En definitiva, captura la idea de que los resultados pueden separarse de lo esperado en relación con la varianza. Entre dos inversiones con el mismo rendimiento esperado, consideraremos más arriesgada la de mayor varianza.

Aplicaciones empresariales

Es obvio que en las innumerables aplicaciones de la estadística al ámbito empresarial el concepto de varianza tiene aplicación. Pero más allá, hay una visión general que ayuda a entender los datos a quienes no son expertos en estadística.

Por ejemplo, imaginemos que estamos viendo un gráfico. Si vemos mucha dispersión (en torno a la media, a una recta de regresión o a lo que se nos muestre en el gráfico) debemos prestar más atención.

La dispersión que muestra la varianza debe incrementar nuestra atención sobre los datos.

Pensemos en unos resultados pasados. Ciertamente, que todos los ejercicios anteriores se hayan movido muy poco de lo previsto no implica que no lo vayan a hacer en el futuro. Sin embargo, cuando observamos mucha variabilidad tenemos que estar más preparados. Es más esperable que haya desviaciones de importancia.

En ocasiones, el problema es que el propio trabajo estadístico no tiene la calidad deseable. En otros casos, se debe, por ejemplo, a limitaciones de las metodologías con las que se trabaja o a carencias en los datos. Quizá el destinatario del informe no lo sepa, pero esa dispersión rara está lanzando una voz de alarma.

Por ello, finalmente, la noción de dispersión nos adentra sobre aspectos como la complejidad o la diversidad. Nos ayuda a poder analizar críticamente los informes y contribuye a que no formemos conclusiones precipitadas.

Nota del editor: Este artículo fue publicado con anterioridad y actualizado a 2023 por su relevancia.