Découvrez les clés de la variance : un concept aux multiples applications dans le monde de la statistique.
- Définition
- Calcul
- Variance d’une variable aléatoire
- Que mesure la variance ?
- Exemples d’application ?
- La variance en finance
- Applications commerciales
La variance est un concept statistique qui nous permet de mieux comprendre les données. D’un point de vue intuitif, elle aide à comprendre la notion de dispersion. D’un point de vue plus formel, elle permet de multiples applications dans le domaine des statistiques.
Quoi qu’il en soit, dans un monde dominé par les données, il s’agit de l’une des premières notions statistiques. Dans le domaine des affaires, elle nous aide à mieux nous exprimer et à tirer plus facilement des conclusions utiles à partir de différents types de rapports.
Qu’est-ce que la variance ?
En termes de statistiques descriptives, la variance peut être définie comme la moyenne des carrés des écarts par rapport à la moyenne. À partir de cette définition, la question peut se poser de savoir pourquoi nous calculons une moyenne des carrés des écarts et non les écarts eux-mêmes.
La réponse est simple. La moyenne des écarts par rapport à la moyenne est toujours nulle. C’est pourquoi nous avons recours à la variance, parfois aussi appelée moment du second ordre centré sur la moyenne.
Prenons un exemple. Imaginons que nous voulions calculer la moyenne de 8, 9 et 10. Nous n’aurons qu’à faire l’addition (ce qui nous donnera 27) et diviser par 3. On voit que la moyenne est de 9. Les écarts seront de -1,0 et 1. La moyenne des écarts est de 0. Quelles que soient les valeurs que nous prenons, le résultat sera toujours le même.
Élever au carré les écarts avant de calculer la moyenne est donc une solution pour éviter que ce calcul soit toujours nul. Rappelons que, que l’écart soit positif, négatif ou nul, le carré n’est jamais négatif. La somme sera supérieure ou égale à zéro. Il ne sera nul que lorsque toutes les valeurs sont égales et qu’il n’y a donc pas d’écart par rapport à la moyenne.
Cependant, en élevant au carré nous élevons également au carré les unités dans lesquelles est mesurée la variance. Par exemple, si la moyenne est en mètres, la variance sera mesurée en mètres carrés. Pour éviter ce problème, nous pouvons extraire la racine carrée de la variance, appelée écart type, qui est utilisée dans de nombreuses situations.
L’écart type est la racine carrée de la variance.
Comment calculer la variance ?
Si nous disposons d’un ensemble de données sur la variable X, sa variance peut être calculée comme suit :
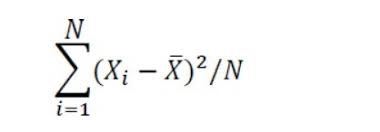
Variance
- xi c’est le numéro de données i.
- x̄ est la moyenne arithmétique.
- N est le nombre de données.
Variance d’une variable aléatoire
Dans le calcul des probabilités, nous pouvons également être intéressés par le calcul de la variance d’une variable aléatoire. Pour ce faire, nous procéderons comme suit :
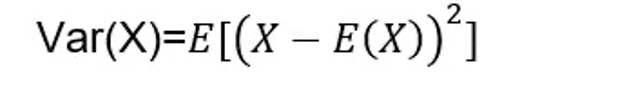
Où :
- Var (X) est la variance de la variable aléatoire discrète X.
- E est l’espérance mathématique.
Si ce que nous avons est une variable aléatoire discrète, ceci est transformé en :
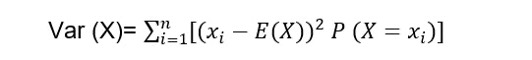
Où :
- E (X) est l’espérance mathématique de la variable aléatoire X.
- P (X = x)i) est la probabilité que la variable aléatoire X prenne la valeur xi.
Dans le cas d’une variable aléatoire continue, nous aurons :
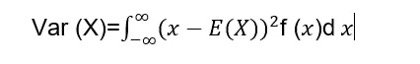
Où :
- E (X) est l’espérance mathématique de la variable aléatoire X.
- f (x) est la fonction de densité de probabilité de la variable aléatoire X.
Que mesure la variance ?
La variance est une mesure de dispersion. Elle saisit dans quelle mesure les données se situent autour de la moyenne. Si nous avons des données très supérieures et très inférieures à la moyenne, la moyenne sera moins représentative, ce qui se traduira par une variance élevée.
Imaginons, par exemple, que nous voulions calculer le salaire moyen de deux entreprises n’employant que deux personnes. Dans l’entreprise A, les salaires sont : 23 500 € et 24 500 €. Dans l’entreprise B, ils sont : 16 000 € et 32 000 €. On voit que, dans les deux cas, la moyenne est la même : 24 000 €. Cependant, cette moyenne est plus représentative pour l’entreprise A, puisque les 2 valeurs sont beaucoup plus proches de la moyenne que dans l’entreprise B.
Dans notre exemple simple, nous n’avons pas eu besoin de calculer la variance pour observer, en un coup d’œil, que la moyenne est plus représentative dans l’entreprise A. Néanmoins, nous aurions pu avoir des centaines, des milliers, des millions de données… Dans ce cas, il est utile d’avoir un chiffre qui nous montre la dispersion.
Cependant, la variance, en elle-même, ne nous dit pas grand-chose. Dans notre exemple, nous comparons deux entreprises avec la même moyenne, mais nous avons besoin d’une valeur pour nous donner plus de contexte. En effet, avec des moyennes différentes, les variances sont forcément différentes. La solution passe par le coefficient de variation :
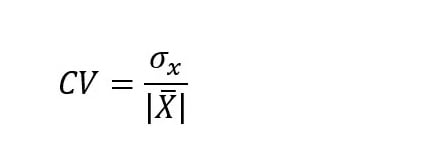
Où :
- σ est l’écart type (racine carrée de la variance).
- x̄ est la moyenne arithmétique.
Ce coefficient a l’avantage d’être un facteur 1 et, par conséquent, il est sans dimension. Il mesure combien de fois l’écart type (racine carrée de la variance) est contenu dans la moyenne.
Exemples d’application
Les applications statistiques du concept de variance sont innombrables. Voici les principales :
- Les estimateurs efficaces. Ce sont ceux dont l’espérance est la vraie valeur du paramètre et qui, en outre, ont une variance minimale. De cette manière, nous réduisons autant que possible le risque que ce que nous extrayons d’un échantillon s’écarte trop de la valeur réelle du paramètre.
- Les estimateurs cohérents. Ce sont ceux qui, à mesure que la taille de l’échantillon augmente, tendent à avoir une variance nulle. Avec de grands échantillons, l’estimation tend à s’écarter très peu de la valeur réelle.
- Dans la distribution normale, la variance (sa racine carrée, l’écart type) est l’un des paramètres. La cloche gaussienne tend à devenir plus haute et plus étroite à mesure que la variance diminue.
- Dans les modèles de régression, nous parlons d’homoscédasticité lorsque la variance de l’erreur est constante sur l’ensemble des observations. Par exemple, dans une régression simple, nous voyons un nuage de points dans lequel la dispersion des points autour de la ligne ou de la courbe estimée reste constante.
- L’analyse de variance (ANOVA) permet de comparer différents groupes et de voir les facteurs qui les influencent.
- L’inégalité de Tchebychev nous permette de déterminer dans quelle mesure une variable aléatoire est susceptible de se séparer de son espérance mathématique proportionnellement à son écart type (racine carrée de la variance).
La variance en finance
En finance, il est habituel de relier la variance au risque. En bref, elle exprime l’idée que les résultats peuvent être séparés des attentes en ce qui concerne la variance. Entre deux investissements ayant la même espérance de rendement, nous considérerons que celui dont la variance est la plus élevée est plus risqué.
Applications commerciales
Il est évident que dans les innombrables applications des statistiques à l’environnement des entreprises, le concept de variance a une application. Mais au-delà, il y a une vue d’ensemble qui aide les non-statisticiens à comprendre les données.
Par exemple, imaginons que nous regardons un graphique. Si nous constatons une grande dispersion (autour de la moyenne, d’une ligne de régression ou de tout autre élément figurant sur le graphique), nous devons être plus attentifs.
La dispersion montrée par la variance devrait accroître notre attention sur les données.
Pensons à certains résultats passés. Certes, le fait que tous les exercices antérieurs n’aient que très peu bougé par rapport à ce qui était prévu ne signifie pas qu’ils ne le feront pas à l’avenir. Cependant, lorsque nous observons une grande variabilité, nous devons être mieux préparés. Il faut plutôt s’attendre à ce qu’il y ait des écarts importants.
Parfois, le problème réside dans le fait que le travail statistique lui-même n’est pas de la qualité souhaitée. Dans d’autres cas, cela est dû, par exemple, à des limitations dans les méthodologies utilisées ou à des lacunes dans les données. Le destinataire du rapport n’en est peut-être pas conscient, mais une dispersion aussi hors-norme tire la sonnette d’alarme. Ainsi, finalement, la notion de dispersion nous amène à des aspects tels que la complexité et la diversité. Cela nous aide à pouvoir analyser les rapports de manière critique et à ne pas tirer de conclusions hâtives.
Ces articles peuvent également vous intéresser :







